SUCESIONES Y SERIES

SUCESIONES Y SERIES NUMÉRICAS

CONCEPTO DE SUCESIÓN: Se define como un conjunto de elementos (números o letras), uno detrás de otro con un cierto orden.

Ejemplos:

                 1, 3, 5, 7, ...                     a, c, e, g...                  2, 4, 6, 8, 10 ....

En este caso cada uno de los elementos de la sucesión se incrementan a razón de 2 unidades y están escritos en forma ascendente. la sucesión puede ser numérica o alfanumérica y los elementos deben aumentar o disminuir a la misma razón. 

TIPOS DE SUCESIONES.

A).- Sucesiones aritméticas: Son aquéllas en las que la razón entre los elementos se obtiene por una  diferencia (resta) o suma, por ejemplo:

                                        

                                      1, 4, 7, 10, ...

En este caso la razón a la que aumentan las cantidades es de 3 unidades, ya que 4-1=3

La regla para obtener un elemento cualesquiera es:

 
La regla es x_n = 3n-2

Por ejemplo si queremos obtener el número que ocupa el lugar x5, tendremos que:

  x5= 3(5)-2 = 15-2=13

Otro ejemplo es la sucesión:

                                          3, 8, 13, 18, ...    

En este caso los números se incrementan a razón de 5 unidades y la 

La regla es x_n = 5n-2

A manera de comprobar la sucesión anterior, podemos encontrar el número que ocupa el sexto lugar:

    X6=5(6)-2 = 30-2 =28

Cabe mencionar que para encontrar cualquiera de los términos de una sucesión aritmética podemos utilizar la siguiente formula: 

                                        

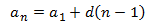
Ejemplo: Podemos calcular el sexto término de la sucesión anterior

                                         a₆= 3 + 5(6-1)

                                         a₆= 3 + 5(5)= 3 + 25 = 28

  

B).- Sucesiones geométricas: Son aquéllas donde la razón entre cada uno de los elementos se obtiene por medio de una multiplicación o una división, por ejemplo:

                            2, 4, 8, 16, ....

En esta sucesión los valores se incrementan a razón de  2 entre cada dos términos y la La regla es x_n = 2ⁿ

Como ejemplo podemos determinar el valor del cuarto elemento de la sucesión:

                                                   X4= 2 elevado a la cuarta potencia

                                                   X4 = 2x2x2x2 = 16

Para encontrar el valor de la razón, también podemos utilizar la siguiente fórmula:

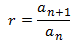
Donde: r = valor de la razón

a(n+1)= valor siguiente

 an= valor actual

A manera de comprobación podemos resolver el ejemplo anterior:

Elegimos las dos primeras cantidades ( 2 y 4)  r= 4/2 = 2

Si elegimos las dos últimas cantidades, tendremos:  16/8 = 2

resultando que es la misma razón entre cada uno de los números.

Para encontrar cualquiera de los términos de una sucesión geométrica, podemos utilizar la siguiente formula:

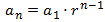
SERIE NUMÉRICA: Se puede decir que, una serie se define como la suma de un conjunto de términos que corresponden a una sucesión. 

Ejemplo:

Sucesión:  1, 2, 3, 4

Serie: 1+2+3+4 = 10

FORMULA PARA ENCONTRAR LA SUMATORIA:

Ejemplos:

Encuentre la suma de los primeros 20 términos de la serie aritmética si a 1 = 5 y a 20 = 62.

Encuentre la suma de los primeros 8 términos de la serie geométrica si a 1 = 1 y r = 2.

             

RAZONES Y PROPORCIONES

Razones y proporciones

Razón: Es el valor que se representa como el cociente entre dos cantidades y de la cual se encuentran valores proporcionales.

Por ejemplo, si en una caja tenemos 24 caramelos y 18 paletas, entonces lo representaremos de alguna de las siguientes formas:

24/18

24:18

Y como la fracción podemos simplificarla, entonces tendremos:

4/3

4:3

Y se lee que existe una razón de 4 a 3, o de 4 por cada 3.

Ahora bien, cada una de las cantidades de una razón tiene un nombre: La cantidad que se encuentra en el numerador se llama antecedente y la cantidad que aparece en el denominador se llama consecuente.

Tipos de razones.

1).- Razón aritmética: Es la comparación de dos cantidades mediante la diferencia o resta. r= a-b   donde a= antecedente    y   b= consecuente

Ejemplos:    12 - 8 = 4            25 - 10 = 15                    6 - 4 = 2

2).- Razón geométrica: Es la comparación de dos cantidades mediante la división o cociente, y consiste en determinar cuántas  veces cada una de las cantidades contiene  a dicha unidad de referencia.

Ejemplos:

La razón entre 6 y 2 es 3 , ya que 6/2 = 3

La razón entre 100 y 10 es 10 , porque 100/10=10

Proporción: Es el valor que indica una igualdad entre dos cantidades y que corresponden a una razón especifica. 

Ejemplo:              2/3 = 6/9   ó   2:3 = 6:9

En este caso las dos cantidades son equivalentes o iguales, resultando la segunda cantidad de multiplicar el numerador y el denominador de la primera por una razón que es el numero 3. Así mismo otro valor proporcional seria 18/27 , que resulta de multiplicar el numerador y denominador de la segunda cantidad por el valor de la razón (3).

Tipos de proporciones.

1).- Proporción directa: Es aquélla donde la cantidad del antecedente aumenta la cantidad del consecuente de manera proporcional.

Ejemplos:

                  1/2 = 3/6           5/8 = 10/16             2/3 = 6/9

2).- Proporción inversa: En esta proporción la cantidad en el antecedente significa la disminución de la cantidad en el consecuente, en este caso se aplica una regla de tres como se muestra en el siguiente ejemplo:

Si 2 agricultores tardan 10 días en arar un campo, ¿Cuanto tardaran 5 agricultores en desarrollar el mismo trabajo?

Solución:

Estamos hablando de una proporción inversa, ya que si aumenta el número de trabajadores el trabajo

se desarrollará en menos tiempo.

Para resolverlo se aplica la regla de tres:

antecedente                consecuente

Y se resuelve:

 días

Es decir, mientras que dos agricultores tardan  días, con la ayuda de otros  compañeros consiguen hacer el mismo trabajo en tan solo  días.   

CALCULO DE PORCENTAJES

CALCULO DE PORCENTAJES

El porcentaje de una cantidad es un recurso matemático, que representa una cantidad dada como una fracción en 100 partes iguales. También se le llama comúnmente tanto por ciento donde por ciento significa «de cada cien unidades». Por ejemplo, si decimos el 25%, esto significa dividir 25/100 = 0.25  que correspondería a la cuarta parte de una cantidad. Si decimos el 50%, esto significa dividir  50/100 = 0.5 que correspondería a la mitad de una cantidad. 

Podemos representar porcentajes en figuras geométricas como se muestra en los siguientes ejemplos:

En el rectángulo el 50% corresponde a la mitad y en fracción se expresa como 1/2. En el circulo estamos representando el 25% que corresponde a 1/4 de la figura.

Ahora bien, si queremos obtener el tanto por ciento de una cantidad solamente se multiplica dicha cantidad por el valor fraccionario que representa dicho porcentaje, por ejemplo:

1).- Obtenga el 25% de 200. 

      Para obtener el resultado multiplicamos 200 por 0.25 y obtenemos:

      200X0.25 = 50

2).- Obtenga el 50% de 250.

       Para obtener el resultado multiplicamos 250 por 0.50  y obtenemos:

       250x0.50 = 125

3).- Obtenga el 12% de 150.

       Para obtener el resultado multiplicamos  150 por 0.12  y obtenemos:

       150X0.12 = 18

Ejemplos de aplicación dentro de la vida cotidiana:

1.- El señor José  fué a la papelería y compró una mochila que tenia el 15% de descuento y dos libretas que tenían el 12% de descuento. Si el precio de la mochila es de $300.00 y el precio de cada libreta es de $48.00 ¿Cuánto pagó en total?

Solución:

Primero calculamos el porcentaje del precio de la mochila: 300x0.15= 45

Como es un porcentaje de descuento, le descontamos $45.00 al precio de la mochila resultando:

Precio de la mochila con descuento= 300-45= $255.00

Ahora obtenemos el porcentaje de descuento de cada libreta:

            48X0.12= $5.76

Precio de la libreta con descuento= 48-5.76=$42.24

Como son dos libretas tenemos: 2X42.24= $84.88

Finalmente, obtenemos la cantidad a pagar:  Mochila    255.00

                                                                       libretas        84.88

Total a pagar:                                                                   339.88

MÍNIMO COMÚN MÚLTIPLO Y MÁXIMO COMÚN DIVISOR.

Mínimo común múltiplo

El mínimo común múltiplo de un conjunto de números es el número mas pequeño que es múltiplo de cada uno de dichos números.

EJEMPLOS:

1).- Hallar el m.c.m de los números    45    10    20

Como primer paso obtenemos la mitad exacta de estos números y los números que no tienen mitad se vuelven a escribir:

      45      5      10

a continuación se obtiene nuevamente la mitad de las cantidades resultantes y se obtiene:

      45      5       5

Ahora se obtiene quinta de los números resultantes, es decir, se dividen entre 5 y se obtiene:      

        9      1       1  

Finalmente se obtiene novena de los números resultantes hasta que la ultima fila sea de unos:

        1       1      1

El mínimo común múltiplo será el producto o multiplicación de los factores por los cuales se dividieron las cantidades, es decir: 

m.c.m = 2X2X5X9 = 180

Nota:  Esto significa que el número 180 es el mínimo común divisible  entre los números 45, 10 y 20

A continuación se muestran mas ejemplos de este tema:

Máximo común divisor

El máximo común divisor de un conjunto de números es el numero mas grande que los divide de manera exacta. En este caso comenzaremos a dividir las cantidades desde el mayor número que las divide a todas las cantidades de manera exacta, si el número no divide a todas las cantidades entonces se anula y se busca otro divisor como se muestra en el siguiente ejemplo:

2).- Hallar el máximo común divisor de los números  45    10    20

Como primer paso buscamos el máximo numero que divide a estas cantidades, que en este caso es el 5 y al dividirlas se obtiene: 

        9        2       4

De las cantidades que resultaron ya no hay otro número que las divida de manera exacta a las tres. Esto significa que el m.c.d. es = 5

A continuación se muestran más ejemplos de este tema:

Obtenga el máximo común divisor de 60    150    y    630

Obtenga el máximo común divisor de   35     70    y    140

Ejercicios propuestos:

Obtenga el mínimo común múltiplo y el máximo común divisor de las siguientes cantidades:

a).-     100     25     12

b).-       75    50      25

c).-     200    78      40

d).-       60    26      15 

e).-       63    25      48