SUMA DE NÚMEROS REALES

SUMA DE NÚMEROS ENTEROS Y FRACCIONARIOS.

REGLA No. 1: Suma de dos o mas números positivos. Se realiza la suma aritmética de las cantidades y el resultado siempre va a ser positivo, por ejemplo:

4 + 6 + 12 = 22

25 + 3 = 28

3/5 + 2/3 = (3)(3) + (5)(2)/ (3)(5) = (9+10)/15 = 19/15

Nota: Cuando sumamos dos números fraccionarios el denominador (numero de abajo) va a ser la multiplicación de los denominadores, en este caso (5)(3)=15 y para obtener la operación del  numerador se multiplican las cantidades en forma cruzada y se suman los resultados (en este caso (3)(3)=9 y (5)(2)=10.

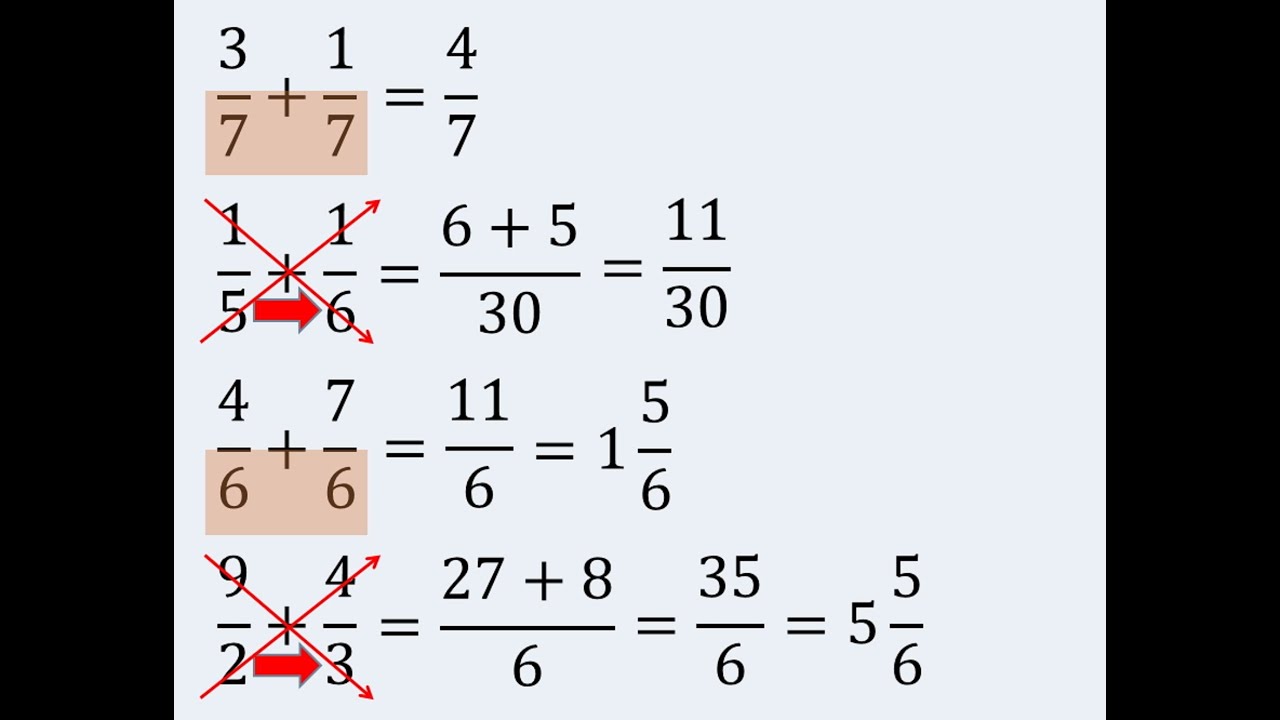
Nota: Cuando los denominadores son iguales, solamente se escribe el numero y no se multiplica y los numeradores se suman.

REGLA No. 2: Suma de dos o mas números negativos. Se realiza la suma aritmética de los valores absolutos de las cantidades y al resultado se le antepone el signo negativo, por ejemplo:

(-8) + (-10) + (3) = - 21

(-15) + (-2) = -17

(-1/2) + (- 6/4)= - 16/8 = -2

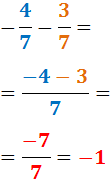
Recordemos que el valor absoluto de un número es la cantidad sin signo y el valor relativo es la cantidad con signo, por ejemplo:

 Cantidad:  - 6        Valor absoluto= 6         Valor relativo= -6

REGLA No. 3: Suma de un número positivo y un número negativo. En este caso la operación se convierte en una resta, entonces al valor absoluto del número mayor se le resta el valor absoluto del número menor y al resultado se le antepone el signo del número mayor. Por ejemplo:

(-12) + 3 = -9

En este caso al 12 se le resta 3 dando como resultado 9 y al resultado se le antepone (-) porque el numero mayor tiene signo negativo.

Ejemplos: 

7+(-2) = 7-2 = 5

Nota importante: Cuando se suman mas de dos números positivos y negativos,se agrupan los números positivos y se desarrolla la suma. A continuación se agrupan los números negativos y se desarrolla la suma, finalmente se realiza la operación de suma de los resultados obtenidos, por ejemplo:

- 10 + 8 + 12 + (-5) + 2 = 22 + (-15) = 22 - 15 = 7

En este caso se agruparon los números negativos: (-10) + (-5) = -15

Se agruparon los números positivos: 8 + 12 +2 = 22

Finalmente se aplicó la regla No. 3:  22 - 15= 7

Ejercicios para resolver:

(-3.25 ) + 4 + ( -2 )=                        (-1/2) + (-7/4)=                   9 + 12 + (-2) + 8 =

(7/6) + (2/3) =                                  12.5 + 3.25 =                     (-8) + ( -3 ) + 10 = 

SISTEMA DE NÚMEROS REALES

SISTEMA DE NÚMEROS REALES

Bienvenidos, comenzaremos con el estudio de los números reales y su clasificación.

Un número real es un número entero o fraccionario positivo, cero o negativo. Este número puede ser racional o irracional. Consideremos que es un número racional puede expresarse como el cociente de dos enteros y el numero irracional no, es un numero indeterminado o no definido. 

El siguiente cuadro sinóptico nos muestra la clasificación de los números reales.

A continuación mostraremos ejemplos de los diferentes tipos de números reales:

Números racionales.

Ejemplos:  5 , 12 , 7 , 11, -3 , -1/2 , 4 1/2 

Números primos: Son aquéllos que solamente son divisibles entre sí mismos y entre la unidad, con respecto a sus factores. Por ejemplo: 1, 2 , 3 , 5, 7....

Recordemos que el número 4 no es primo porque es divisible entre sí mismo, entre 1 y entre 2, esto significa que es divisible entre tres factores que son el 1, el 4 y el 2.

El numero 2 si es primo porque solamente es divisible entre sí mismo (2) y entre la unidad.

El numero 6 no es primo porque es divisible entre mas de dos factores ( entre 6, 1,3 y 2).

Fracciones propias: Son aquéllas donde el numerador es menor que el denominador, por ejemplo: 2/4 , 4/8, 1/2  (recordemos que el numerador es el número de arriba y el denominador el numero de abajo).

Fracciones impropias: Son aquéllas donde el numerador es mayor que el denominador, por ejemplo: 8/3 , 12/4, 25/4 , etc.

Fracciones mixtas: Son aquéllas que están formadas por un número entero y una parte fraccionaria, por ejemplo: 4 1/2  ,  8 1/4  , 6 1/3

Números irracionales.

Pueden ser números  algebraicos irracionales o números no determinados como por ejemplo: La raíz cuadrada de un numero negativo ( numero imaginario ), el valor π (pi): 3.141592653589

1. √5: 2.2360679775
2. √2: 1.41421356237

1.